A Beginner-Friendly Walkthrough of SVD Using Movie Recommendations

A Beginner-Friendly Walkthrough of SVD Using Movie Recommendations

August 1, 2025

My goal here is to explain SVD in a way that helps us understand the core concept and recognise where and how to apply it, without getting lost in complex mathematical details.

---

What is SVD?

SVD (Singular Value Decomposition) is a fundamental concept in linear algebra. It is a form of matrix decomposition. Matrix decomposition involves breaking down a large, complex matrix into simpler components that are easier to analyse and interpret.

SVD is widely used in recommendation systems across domains. For example:

• Product recommendations in e-commerce
• Movie suggestions on streaming platforms
• Content personalisation on news and social media apps
• Matching candidates to jobs on recruiting platforms

Imagine a matrix where each row represents a user and each column represents a movie. The cells contain ratings if the user has seen and rated the movie. Blanks(?) mean that the user has not seen and rated the movie.

SVD helps in predicting the missing values by uncovering hidden patterns in the data.

---

Latent Factors

These hidden patterns, also known as latent factors, are not explicitly labeled. They might correspond to:

• Preference for action versus drama
• Love for indie films versus blockbuster hits
• Enjoyment of complex, plot-driven narratives versus light-hearted comedies
• Interest in animated or family-friendly content versus darker, mature themes
• Favouring fast-paced thrillers over slow-burn character studies

SVD is an unsupervised technique, meaning it does not rely on labeled data or predefined categories.

What makes SVD powerful is that it learns these patterns automatically from the data. It does not require labeled metadata like genres, tags, skills, or job categories. It relies solely on the structure of past interactions to make meaningful predictions.

---

A Bit of Math

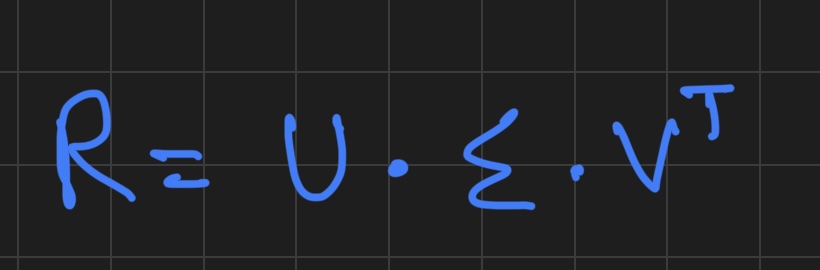
Where:

• R is the original user-item matrix.
• U represents each user's relationship to the latent features.
• Σ (Sigma) is a diagonal matrix that contains weights of each latent feature.
• Vᵀ (V transpose) is a matrix that represents items (movies). Each row is a latent feature, and each column is a movie. It tells us how strongly each movie is associated with each latent pattern.

---

Seeing SVD in Action

To explore these concepts more deeply, I’ve created a hands-on demo that walks through how SVD powers movie recommendations. You can run the project to view full predictions, rating breakdowns, and see how latent factors shape recommendations. Check it out here: GitHub – SVD Educational Demo

The demo uses a simple 6-user, 8-movie dataset where you can see every step of the SVD process:

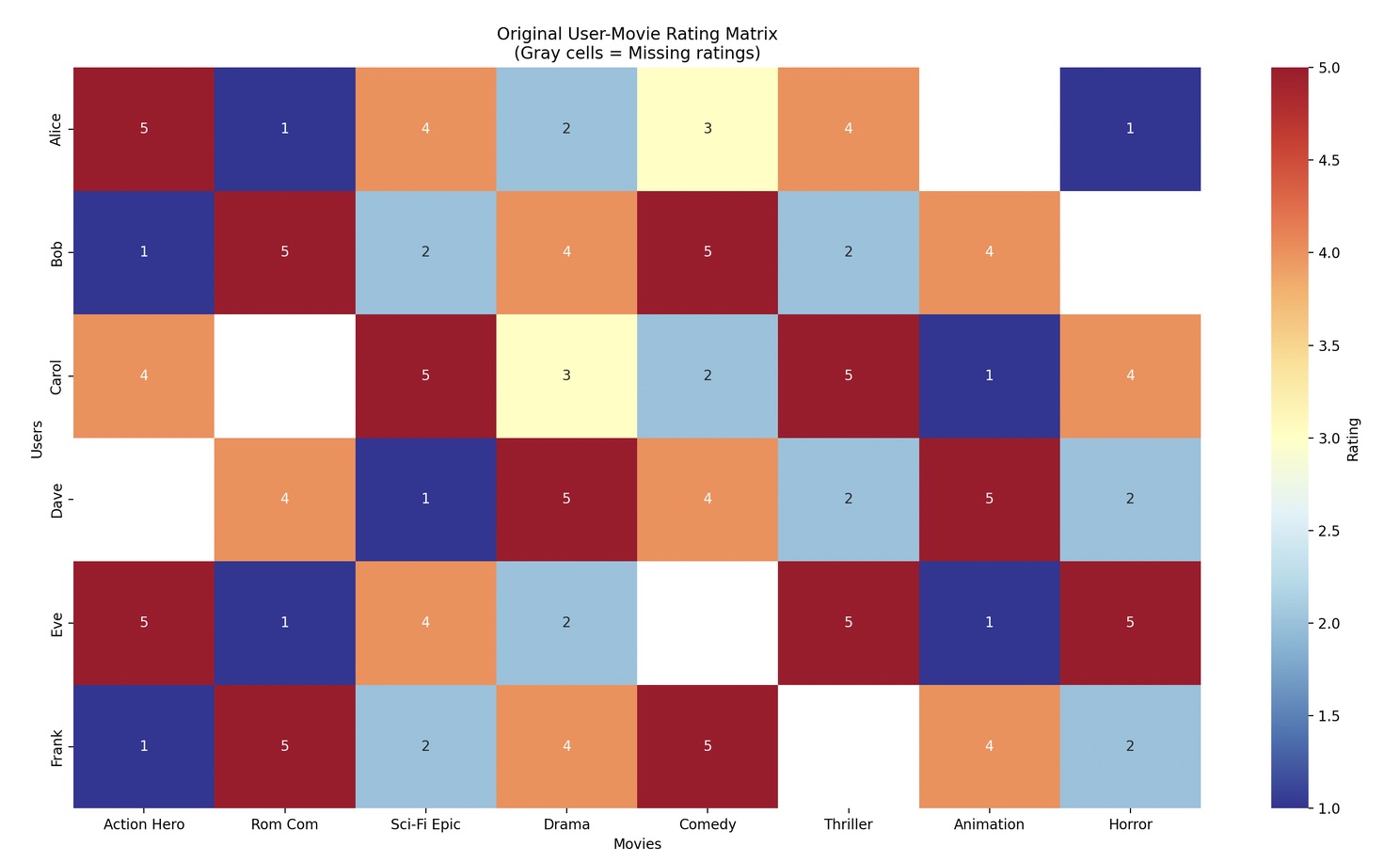
Step 1 – The Original Matrix

Starting with our user-movie rating matrix with missing values (the ? marks from our earlier example).

Step 2 – SVD Decomposition

Watch as SVD breaks down the matrix into U, Σ, and Vᵀ components, with clear heatmap visualisations showing the numerical values.

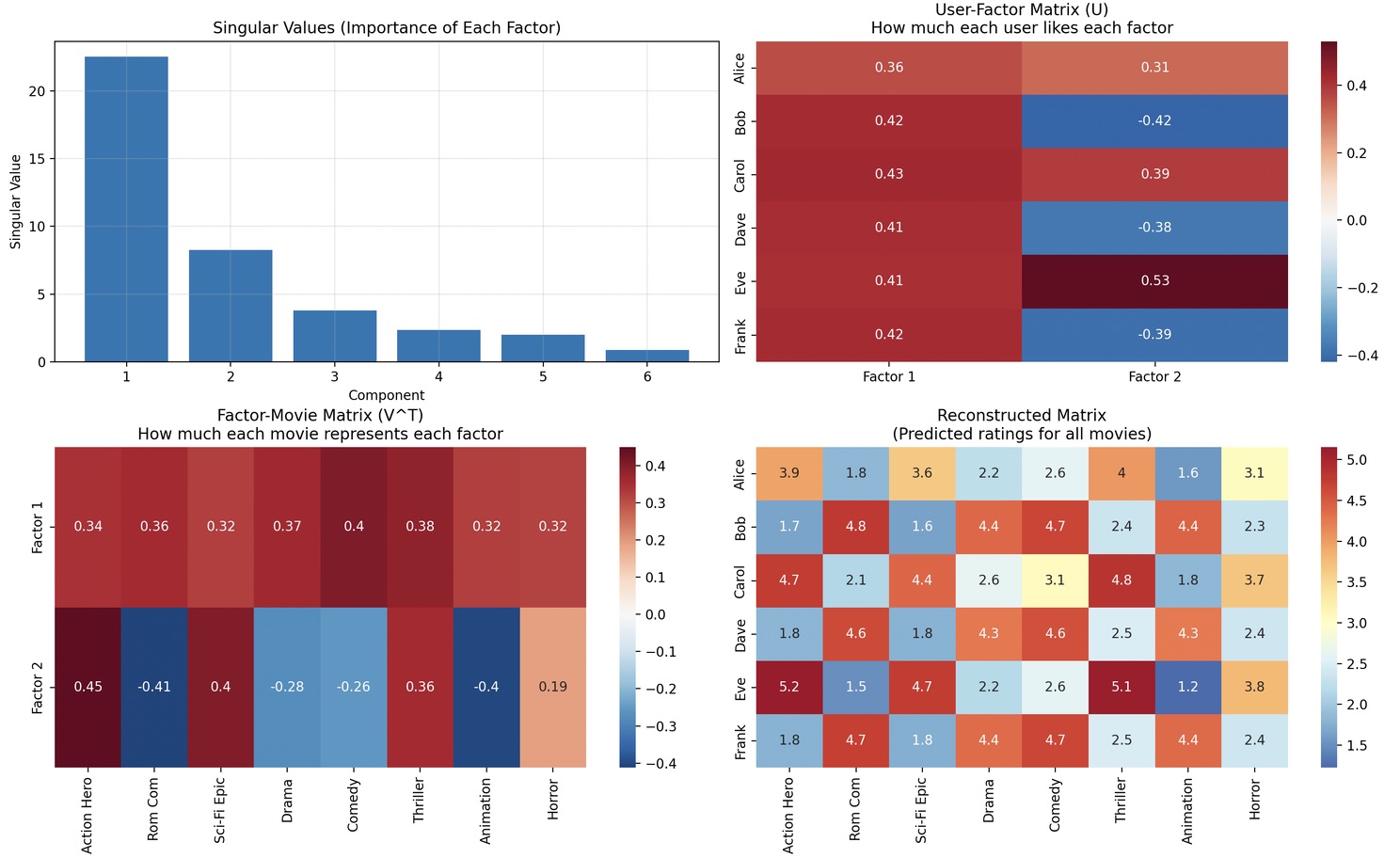
Step 3 – Discovering Latent Factors

The demo reveals what the hidden patterns actually represent:

• Factor 1: Action/Thriller vs Romance/Comedy preference
• Factor 2: Mainstream vs Niche content preference

Step 4 – Making Predictions

See exactly how these factors combine to predict missing ratings and generate recommendations.

---

Why This Matters

Instead of treating SVD as a "black box," you can see:

• The exact numerical decomposition – Every matrix value is visible
• Factor interpretation – What each latent dimension means
• Prediction explanation – Why specific movies are recommended
• Real calculations – How factors combine for final ratings

---

Key Takeaways

SVD's power lies in its ability to find meaningful patterns without being told what to look for. It doesn't need genre labels or movie metadata, it discovers that some users prefer action over romance, or mainstream over niche content, purely from rating patterns.

This same principle applies whether you're recommending products, matching job candidates, or personalising content.

---

#RecommendationSystem #SVD #MatrixFactorization #MachineLearning #ExplainableAI #LearningByBuilding #AIForEveryone #DemystifyingAI